
Cirqits is a puzzle game that we released in early 2020 on iOS (Update: Now available on Android as well!). The game presents you with different multi-faced solid shapes; each face has a particular arrangement of links on it, which can be freely rotated. When a lit face is properly linked to an adjacent face, the second face lights up as well. The objective is find the proper orientation of all of a puzzle’s faces such that everything is linked and lit.
The core idea behind the game came to me and my daughters while we were playing other games with similar tile-rotation mechanics, but in the conventional two-dimensional format. As we were also heavily into origami at the time, it occurred to us that the gameplay mechanic could also work well with polyhedra in three dimensions.
The concept was sound. There were many challenges to overcome, though none were insurmountable. Fortunately they were all the types of problem that I enjoy thinking through. The big ones included:
- How should the base shapes be defined and encoded (the Cube, Hexaball, Dodecahedron, etc)?
- How should the 3D models be made, considering the different visual themes?
- How should the puzzles be created? By puzzles I am referring to “the links on each face such that there is at least 1 solution.”
The Base Shapes
The first question to hurdle was how to define and encode the base shapes in a simple, flexible, and serializable way. (“Serializable” in this context refers to how something can be expressed unambiguously as a piece of text.) It needed to meet these criteria to allow the saving and restoration of game state, and also to facilitate the automatic generation of the puzzle itself – that is, the game could look at the layout and figure out which faces connected to which.
The answer was fairly straightforward. As a child, I spent a lot of time drawing diagrams of “unwrapped” cubes, tetrahedrons, and other polyhedra, and cutting them out and folding them into shape, so expressing the base shapes as flat arrangements of linked polygons became a natural approach.


Above are a couple of pages from my hand-drawn notes in late 2019 where I was working out how the shapes would be laid out. For the game, I then created a small program that would facilitate the layout and encoding of these base shapes. After shape layouts are made by building polygons out from another polygon’s edges and designating fold angles, the tool would encode the layout into a bit of text that concisely described the number of sides in a given polygon, the polygons attached to it, the number of sides of those polygons, and so on. For instance, a 1x1x1 cube would be encoded as “a square, with each edge having another square folded at 90 degrees, with one of those four squares having another square folded at 90 degrees at the opposite edge.”

The 3D Models
After settling the question of the base shapes, it was time to bridge these base shapes to the actual 3D meshes that the game will use to present the puzzle to the player, in all their full visual detail.
The obvious approach would have been creating each mesh in a dedicated 3D modeling program such as Blender and then importing these into Unity. However, this would not have scaled well:
- Reconciling each mesh with the underlying gameplay logic (so that the right things would be rotating by the right amounts to connect to the right adjacent faces) would have been tedious and also introduce lots of fuzziness in the math due to floating point issues, which could lead to seam tearing (i.e. “cracks” in the graphics that occur due to edges not lining up perfectly).
- I would have to create meshes for each combination of base shape and theme (again, tedious), PLUS, for each theme, also create meshes for every possible face permutation. The pentagon face (used in the Dodecahedron and Star shapes) has at least 1 and at most 5 links, making 7 possible permutations (after discounting permutations that are rotated versions of other permutations).
- Every time I change the design, I’d have to manually redo all of the above.
Given 13 shapes and 5 themes, the numbers added up really fast. Therefore, procedural generation—constructing meshes by having the code calculate coordinates for each vertex and triangle in real-time—became the only approach that would not lead to madness. Procedural generation is hard work at first, but this is “front-loaded” effort that, once done, scales easily to any application: after writing the code to generate the triangles needed for, say, the fluted bezels of Ref 708, translating and mapping them to any face in any shape could be seamlessly done at runtime. Adjusting a theme—say, adjusting the height of the bezel—would then be just a matter of adjusting a single value in code.


Puzzle Generation
Similar to the above, manually creating each puzzle (that is, the arrangement of links on faces such that a solution is feasible) was not an option I entertained. While doing so would have allowed “trick puzzles” or those with aesthetically pleasing/surprising solutions, such as a single long snaking and circular path, I wanted to prioritize replayability by having the game dynamically generate puzzles.
As it turned out, this type of problem, which can be called graph traversal, has been extensively studied and several algorithms exist for the generation of “mazes”—that is, node graphs where all nodes are linked together—according to different parameters, such as your preferences for dead ends and straight lines. In the end, I settled on two algorithms, Kruskal’s Algorithm, and a “recursive depth-first” approach, that offered good enough variety and solvability. Furthermore, upon startup, the game estimates the difficulty level of each combination of 3D shape and algorithm, and sorts them accordingly, to generate a mapping of the player’s streak length, and the appropriate combinations of shape and maze algorithm to use: the more you solve in a row, the harder the puzzles that will be presented.
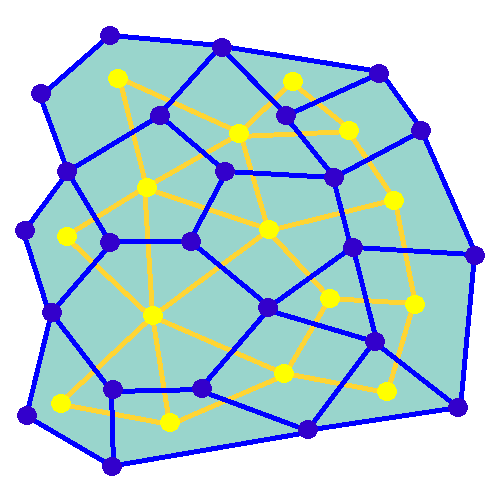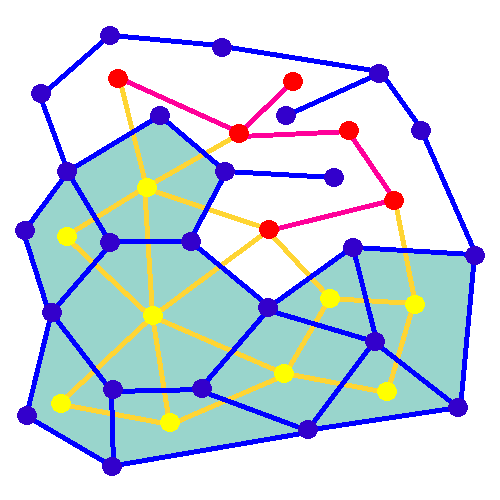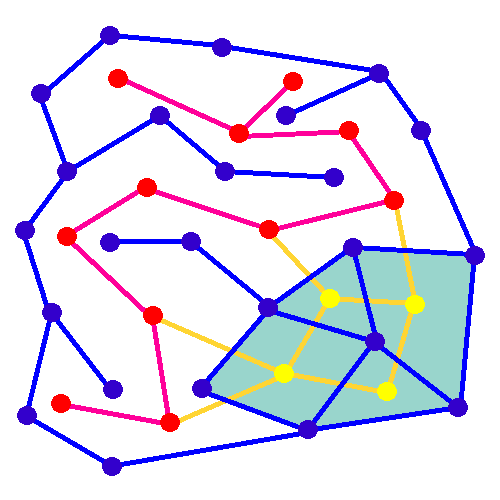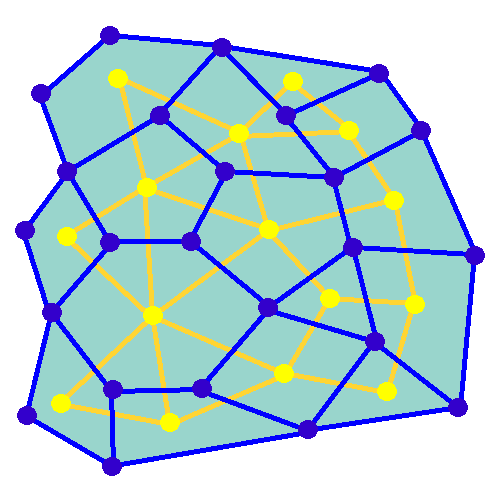
Credit: Nbeverly via Wikipedia
Another benefit of setting up the internal code so that the puzzle algorithm implementations are independent and modular was that, later on, additional algorithms could be added easily, and the game would automatically know how to use them and map them to the difficulty ladder.

Other Stuff
Aside from these there were other, smaller, but no less fun problems to solve:
- The determination of colors for the different faces in the Pop theme is done by an implementation of the Welsh Powell graph coloring algorithm, such that no two adjacent faces have the same color. (If this fascinates you, I suggest reading up on the four color theorem which states that for any map or diagram where shapes are contiguous to one another, one only needs up to four colors.)
- UPDATE (14 Mar 2021) to the above point: I just found that the game’s coloring algorithm, when applied to the Dodecahedron shape, results, in many cases, in 2 or 3 adjacent faces having the same color. Upon reviewing the literature, it turns out that the Welsh Powell algorithm (which I also previously typed as “Walsh-Powell”…*facepalm*) does NOT guarantee satisfying both the “no adjacent faces having the same color” and the “four colors or less” objectives simultaneously. In fact, it looks like, in the worst cases, the algorithm will need d + 1 colors, where d represents the degree of the shape, or the highest number of sides for any face (in Dodecahedron’s case, the degree would be 5). And because I only supplied 4 color options, the algorithm settles for an imperfect solution. Color me surprised. Adding this to my list of fixes to make for the next update…
- The glow effect on the default theme was inspired by the Northern Lights, which my wife and I were fortunate enough to have experienced in Iceland. The effect is achieved through procedural generation of “glow meshes” which are then rendered using custom shaders that deform the mesh and modify its texture in real-time to make the green glow appear to dance.

Epilogue
I read somewhere that “all art is autobiographical,” and while I wouldn’t presume to claim that Cirqits is art, I have indeed come to recognize its autobiographical nature. As I designed and developed it, different bits of inspiration and insight came together from different facets of my life, from making shapes with paper and tape as a child, to my lifelong love of puzzles and games, to my appreciation of how physical, tactile things come together (the Ref 708 theme was inspired by my watch), to my experiences of traveling, photography, and fatherhood.